Fib = (Fibs !!) Where Fibs = 0 : Scanl (+) 1 Fibs

Implementing the Fibonacci sequence is considered the "Hello, world!" of Haskell programming. This page collects Haskell implementations of the sequence.

1 Naive definition
2 Linear operation implementations
- 2.1 With state
  - 2.1.1 Tail recursive
  - 2.1.2 Monadic
- 2.2 Using the infinite list of Fibonacci numbers
  - 2.2.1 Canonical zipWith implementation
  - 2.2.2 With direct self-reference
  - 2.2.3 With scanl
  - 2.2.4 With unfoldr
  - 2.2.5 With iterate
- 2.3 A version using some identities
3 Logarithmic operation implementations
- 3.1 Using 2x2 matrices
- 3.2 Another fast fib
- 3.3 Fastest Fib in the West
4 Constant-time implementations
- 4.1 Using Binet's formula
5 Generalization of Fibonacci numbers
- 5.1 Fibonacci n-Step Numbers
6 See also

Naive definition

The standard definition can be expressed directly:

            fib            0            =            0            fib            1            =            1            fib            n            =            fib            (            n            -            1            )            +            fib            (            n            -            2            )

This implementation requires O(fib n) additions.

Linear operation implementations

With state

Haskell translation of python algo

            {- def fib(n):                          a, b = 0, 1                          for _ in xrange(n):                          a, b = b, a + b                          return a  -}

Tail recursive

Using accumulator argument for state passing

            {-# LANGUAGE BangPatterns #-}            fib            n            =            go            n            (            0            ,            1            )            where            go            !            n            (            !            a            ,            !            b            )            |            n            ==            0            =            a            |            otherwise            =            go            (            n            -            1            )            (            b            ,            a            +            b            )

Monadic

            import            Control.Monad.State            fib            n            =            flip            evalState            (            0            ,            1            )            $            do            forM            [            0            ..            (            n            -            1            )]            $            \            _            ->            do            (            a            ,            b            )            <-            get            put            (            b            ,            a            +            b            )            (            a            ,            b            )            <-            get            return            a

Using the infinite list of Fibonacci numbers

One can compute the first n Fibonacci numbers with O(n) additions. If fibs is the infinite list of Fibonacci numbers, one can define

Canonical zipWith implementation

            fibs            =            0            :            1            :            zipWith            (            +            )            fibs            (            tail            fibs            )

With direct self-reference

            fibs            =            0            :            1            :            next            fibs            where            next            (            a            :            t            @            (            b            :            _            ))            =            (            a            +            b            )            :            next            t

With scanl

            fibs            =            scanl            (            +            )            0            (            1            :            fibs            )            fibs            =            0            :            scanl            (            +            )            1            fibs

The recursion can be replaced with fix :

            fibs            =            fix            (            scanl            (            +            )            0            .            (            1            :            ))            fibs            =            fix            ((            0            :            )            .            scanl            (            +            )            1            )

The fix used here has to be implemented through sharing, fix f = xs where xs = f xs, not code replication, fix f = f (fix f), to avoid quadratic behaviour.

With unfoldr

            fibs            =            unfoldr            (            \            (            a            ,            b            )            ->            Just            (            a            ,(            b            ,            a            +            b            )))            (            0            ,            1            )

With iterate

            fibs            =            map            fst            $            iterate            (            \            (            a            ,            b            )            ->            (            b            ,            a            +            b            ))            (            0            ,            1            )

A version using some identities

            fib            0            =            0            fib            1            =            1            fib            n            |            even            n            =            f1            *            (            f1            +            2            *            f2            )            |            n            `            mod            `            4            ==            1            =            (            2            *            f1            +            f2            )            *            (            2            *            f1            -            f2            )            +            2            |            otherwise            =            (            2            *            f1            +            f2            )            *            (            2            *            f1            -            f2            )            -            2            where            k            =            n            `            div            `            2            f1            =            fib            k            f2            =            fib            (            k            -            1            )

This seems to use 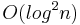$O(log^2 n)$ calls to fib.

Logarithmic operation implementations

Using 2x2 matrices

The argument of iterate above is a linear transformation, so we can represent it as matrix and compute the nth power of this matrix with O(log n) multiplications and additions. For example, using the simple matrix implementation in Prelude extensions,

            fib            n            =            head            (            apply            (            Matrix            [[            0            ,            1            ],            [            1            ,            1            ]]            ^            n            )            [            0            ,            1            ])

This technique works for any linear recurrence.

Another fast fib

(Assumes that the sequence starts with 1.)

            fib            =            fst            .            fib2            -- | Return (fib n, fib (n + 1))            fib2            0            =            (            1            ,            1            )            fib2            1            =            (            1            ,            2            )            fib2            n            |            even            n            =            (            a            *            a            +            b            *            b            ,            c            *            c            -            a            *            a            )            |            otherwise            =            (            c            *            c            -            a            *            a            ,            b            *            b            +            c            *            c            )            where            (            a            ,            b            )            =            fib2            (            n            `            div            `            2            -            1            )            c            =            a            +            b

Fastest Fib in the West

This was contributed by wli (It assumes that the sequence starts with 1.)

            import            Data.List            fib1            n            =            snd            .            foldl            fib_            (            1            ,            0            )            .            map            (            toEnum            .            fromIntegral            )            $            unfoldl            divs            n            where            unfoldl            f            x            =            case            f            x            of            Nothing            ->            []            Just            (            u            ,            v            )            ->            unfoldl            f            v            ++            [            u            ]            divs            0            =            Nothing            divs            k            =            Just            (            uncurry            (            flip            (,))            (            k            `            divMod            `            2            ))            fib_            (            f            ,            g            )            p            |            p            =            (            f            *            (            f            +            2            *            g            ),            f            ^            2            +            g            ^            2            )            |            otherwise            =            (            f            ^            2            +            g            ^            2            ,            g            *            (            2            *            f            -            g            ))

An even faster version, given later by wli on the IRC channel.

            import            Data.List            import            Data.Bits            fib            ::            Int            ->            Integer            fib            n            =            snd            .            foldl_            fib_            (            1            ,            0            )            .            dropWhile            not            $            [            testBit            n            k            |            k            <-            let            s            =            bitSize            n            in            [            s            -            1            ,            s            -            2            ..            0            ]]            where            fib_            (            f            ,            g            )            p            |            p            =            (            f            *            (            f            +            2            *            g            ),            ss            )            |            otherwise            =            (            ss            ,            g            *            (            2            *            f            -            g            ))            where            ss            =            f            *            f            +            g            *            g            foldl_            =            foldl'            -- '

Constant-time implementations

The Fibonacci numbers can be computed in constant time using Binet's formula. However, that only works well within the range of floating-point numbers available on your platform. Implementing Binet's formula in such a way that it computes exact results for all integers generally doesn't result in a terribly efficient implementation when compared to the programs above which use a logarithmic number of operations (and work in linear time).

Beyond that, you can use unlimited-precision floating-point numbers, but the result will probably not be any better than the log-time implementations above.

Using Binet's formula

            fib            n            =            round            $            phi            **            fromIntegral            n            /            sq5            where            sq5            =            sqrt            5            ::            Double            phi            =            (            1            +            sq5            )            /            2

Generalization of Fibonacci numbers

The numbers of the traditional Fibonacci sequence are formed by summing its two preceding numbers, with starting values 0 and 1. Variations of the sequence can be obtained by using different starting values and summing a different number of predecessors.

Fibonacci n-Step Numbers

The sequence of Fibonacci n-step numbers are formed by summing n predecessors, using (n-1) zeros and a single 1 as starting values: 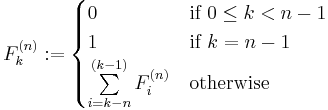$F^{(n)}_k := \begin{cases} 0 & \mbox{if } 0 \leq k < n-1 \\ 1 & \mbox{if } k = n-1 \\ \sum\limits_{i=k-n}^{(k-1)} F^{(n)}_i & \mbox{otherwise} \\ \end{cases}$

Note that the summation in the current definition has a time complexity of O(n), assuming we memoize previously computed numbers of the sequence. We can do better than. Observe that in the following Tribonacci sequence, we compute the number 81 by summing up 13, 24 and 44:

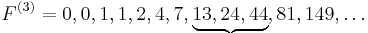
$F^{(3)} = 0,0,1,1,2,4,7,\underbrace{13,24,44},81,149, \ldots$

The number 149 is computed in a similar way, but can also be computed as follows:

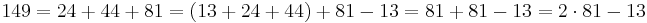
$149 = 24 + 44 + 81 = (13 + 24 + 44) + 81 - 13 = 81 + 81 - 13 = 2\cdot 81 - 13$

And hence, an equivalent definition of the Fibonacci n-step numbers sequence is:

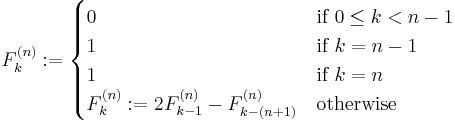
$F^{(n)}_k := \begin{cases} 0 & \mbox{if } 0 \leq k < n-1 \\ 1 & \mbox{if } k = n-1 \\ 1 & \mbox{if } k = n \\ F^{(n)}_k := 2F^{(n)}_{k-1}-F^{(n)}_{k-(n+1)} & \mbox{otherwise} \\ \end{cases}$

(Notice the extra case that is needed)

Transforming this directly into Haskell gives us:

            nfibs            n            =            replicate            (            n            -            1            )            0            ++            1            :            1            :            zipWith            (            \            b            a            ->            2            *            b            -            a            )            (            drop            n            (            nfibs            n            ))            (            nfibs            n            )

This version, however, is slow since the computation of nfibs n is not shared. Naming the result using a let-binding and making the lambda pointfree results in:

            nfibs            n            =            let            r            =            replicate            (            n            -            1            )            0            ++            1            :            1            :            zipWith            ((            -            )            .            (            2            *            ))            (            drop            n            r            )            r            in            r